《Cognitive Electronic Warfare An Artificial Intelligence Approach》第六章的读书笔记。

六、电子战管理（EBM）

目录

EBM系统计划部署多少个节点，每个节点获得哪些资源。电子战计划包括确定任务、资源、评估威胁。影响计划的因素包括可用资源、预期效果、位置限制(海拔、射程、时间或载荷)等。

6.1节介绍了人工智能规划方法，讨论了不确定性、资源分配和多时间尺度等问题。6.2节是团队协调的博弈论方法和对抗性行为的推理。6.3节讨论人机界面(HMI)，包括如何利用人类认知、提取目标以及向人类用户解释决策。

在一个完整的电子战系统中，将会有多个决策者。计划是针对特定任务的，在地理上或时间上是分开的。这种分离可以简化系统设计。

6.1 计划

与优化(optimization)和调度(scheduling)相比，计划（planning）范围更广，时间更长。在更长的时间范围内评估行动，并处理更广泛的资产和资源类型。

计划侧重于实现目标所需的一系列行动的因果推理。计划通常是一组不指定资源或时间表的动作；调度将时间和资源分配给该计划。

经典计划将当前情况(初始状态)的描述、一组行动和目标描述作为输入，输出是从当前情况到目标的一系列行动。

概率规划处理不确定的环境，时间规划处理持续的动作，两者可以并行。时间规划技术通常处理资源，因为资源使用在本质上经常是临时的。条件计划生成具有条件分支的计划：它生成基于对环境的感知来选择行动的应急计划。

搜索和规划算法的判断依据是完备性、可操作性、时间复杂性和空间复杂。本章介绍了以慎重(deliberately)的方式在解空间中搜索的算法。

6.1.1 规划基础知识：问题定义和搜索

问题可以用以下组成来正式定义：

• 初始状态，$S_0∈S$；

• 一组可能的行动，$A$；

• 每个动作的操作说明，状态$s$中执行动作$a$所产生的结果)的函数，$ρ：(s，a)→s’$，

• 目标状态，$s_g∈S$；

• 为状态$c(s，a，s')$之间的每个步骤分配成本的成本函数。

问题$P$的解决方案是从$S_0$中找到状态序列$(s_1,s_2,...，s_g)$的动作序列$π=(a_1,a_2,...，a_n)$。最优解具有从$s_0$到$s_g$的最低成本。

经典的规划域通常用Planning Do-main Definition Language(PDDL)表示。PDDL语法对域的内容进行编码：状态、动作等。状态表示为$(arg1，...，argN)$，例如$s=in(pilot、airplane)AND has fuel$。动作具有前提条件，只有当动作$A$的前提条件文字$p_i∈s$为真时，该动作$a$才适用于状态$s$。PDDL捕获了复杂性不同的规划问题，包括约束、条件效应、数值和时间特征以及行动成本。

搜索算法创建以初始状态为根的搜索树来查找操作序列。每个分支步骤通过将每个动作应用于该状态来扩展当前状态，生成新状态。例如，一个在网格世界中移动的简单机器人可以移动到任何相邻的网格正方形，从而产生四种可能的未来状态。连续值可以离散化，也可以用均值和方差等统计数据表示。修剪步骤(Pruning steps）消除了非法或重复的状态，以减少搜索工作。

不知情搜索策略算法在没有指导的情况下构建这棵搜索树，扩展节点直到它们到达目标。常用的搜索策略包括广度优先搜索、深度优先搜索、迭代加深搜索和双向搜索。

知情搜索策略使用启发式算法来指导搜索，从而使搜索更有效率或更有效。启发式规则可以由专家生成，也可以由机器学习根据经验数据创建。最著名的启发式算法之一是$A^*$。5.2节中的许多调度器也使用启发式算法。

6.1.2 分层任务网络

分层任务网络(HTN)：HTN不是通过改变模型的状态来搜索目标，而是定义一组要完成的抽象任务，以及每项任务的方法，这些方法代表了执行这些任务的不同方式。动作之间的依赖关系用层次结构的网络表示。

HTN规划者在不断提高的抽象层次上制定计划。HTN是实际应用中使用最广泛的规划形式，原因：它可以有效地管理计算复杂性；它符合人类思考问题的方式。这一特征意味着人类可以更容易地描述任务之间的关系，并在用户界面解释任务进度。

HTN规划者在任务网络上进行推理。网络是要执行的任务和相关约束的集合，如图所示：

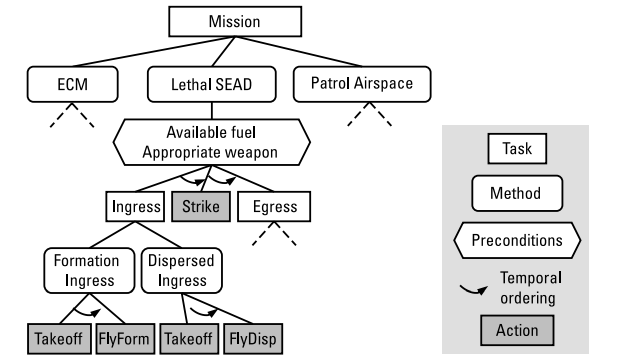
有三种类型的任务：

• 目标任务，捕获所需的结束状态；

• 原语任务，可以在状态下直接执行的动作；

• 前提条件和预期效果；

• 复合任务，展示如何通过原始任务实现目标。可以将复合任务分解为偏序子任务(基元或复合)。

因此，HTN问题的解决方案是基元任务的可执行序列，该基元任务序列可以通过将复合任务分解成一组更简单的任务，并通过插入排序约束来从初始任务网络获得。

HTN计划算法应用于：医学、生产计划、后勤、危机管理、空中战役计划、海军指挥与控制、航空母舰调度和无人作战机器人小组等。

6.1.3 行动不确定性

当动作具有非确定性结果时，有几种规划方法：条件规划、图规划、随机可满足性、一阶决策图和MDP。其中MDP使用最广泛。

MDP是在不确定情况下建模和指导顺序DM的框架。马尔可夫模型描述了在有限状态集之间概率转移的系统。

转移概率$P(s'|s，a)$扩充了6.1.1节的问题定义，转移概率$P(s’|s，a)$表示如果在状态$s∈S$中进行动作$a∈A$达到状态$s'∈S$的概率。当动作$a$在状态$s$中进行时，收益$R$描述预期收益。如果对手行为模型可从ES获得，则它们可以被合并到转移函数中，以反映威胁状态。

策略$π$指定节点应在每个状态下执行的操作；$π(S)$是$π$为状态$s$建议的操作。在固定策略中，一旦找到策略，每个状态的操作都是固定的；在非固定策略中，策略随时间变化。

因为环境是随机的，所以策略的质量是通过多次执行策略的预期效用来衡量的。最优策略$π^∗$是产生最高预期效用的策略。

MDP最常见的效用函数是discounted rewards，其中状态序列的效用随着时间的推移对折扣因子$γ∈[0，1]$进行折扣。从状态$S_0$开始的策略$π$的预期效用为：

$$U^{\pi}(s_0)=E[\sumγ^{i}R(s_i,a_i)]$$

式中$a_i=π^{*}(s_i)$。$π^{*}(s_i)$是使后续状态$s_{i+1}$的效用最大化的动作。

适合任务的行动选择可能包括：

• 最大限度：选择预期回报最大的行动，即使它有风险。

• 最大可能性：通过概率和预期收益来选择期望值最大的行动。

• 最大值：选择最小值最大的动作。

• 最小限度的损失：选择将最坏情况下的损失降至最低的行动(规避风险)。

MDP计划在计算上非常低效，但MDP是制定概率计划的最广泛使用的框架。

6.1.4 信息不确定性

在复杂的环境中，信息不能完全了解。决策引擎必须推测信息中的不确定性。有了这些信息，规划者可以使用主动感知和通信来提高信息质量或确定性。管理信息不确定性的方法包括：

• (Dempster-Shafer)理论，衡量人们对一个事实的信任程度，并计算证据支持该命题的概率；

• 模糊逻辑，代表事实的真值；

• 论证，明确构建连接证据和结论的关系。

这些方法支持评估信息的效用，使人们能够慎重考虑信息。

节点可以交换观察结果和决策，以改进它们对情况的理解。数据融合解决了模糊性，减少了模型中的不确定性。

节点通信的详细程度决定了它们可以实现的协调程度，以及它们可以执行的协调动作的种类和成本。节点也可以使用隐式通信来发送信息。该方法假设其他节点可以观察到状态的动作或改变，并推断发生了什么，而不需要显式交互。

6.1.5 时间规划和资源管理

节点是异构的，资源是受限的，分布式任务必须协调。将规划与资源管理结合起来，确保了资源优化和电子战战略的统一。规划者必须根据任务模型，在需要资源的时间范围内，最大限度地利用资源来处理当前和预期的威胁。

在现实中，约束性要求通常是相互矛盾的。雷达技术系统工程通过匹配系统的不同硬件和软件组件来处理这些约束，以在折衷中满足需求。

规划者通过(1)跟踪资源使用情况；(2)确定哪些信息需要共享；(3)以高效的方式共享信息来实现确保资源的可用性。

6.1.6 不同时间尺度

决策有不同的应用期；动作有不同的持续时间；度量指标有不同的延迟。

最有效的方法是完全分离计划器，例如，一个计划器以天为单位运行，第二个以分钟为单位运行，第三个以毫秒为单位运行。时间抽象层的每一层都对下面的层施加约束。该方法易于设计、实现和测试，并且支持不同规模的专业推理。

6.2 博弈论

博弈论是一种分析工具，用于模拟多个实体之间战略性的、复杂的互动。博弈论支持不确定环境中的决策制定，一个行动结果的不确定性取决于其他人的反应。

博弈论的特点是既有合作又有竞争，它对于合作团队、资源分配和对抗环境都是有效的。

合作博弈允许个人在选择行动之前达成协议，而非合作博弈则是自私但理性的个人立场。

在团队合作的背景下，博弈论构建了自组织的、分散的网络，在这种网络中，每个人都有自己的利益，但必须合作才能最大限度地发挥作用。博弈论已经应用于射频领域的功率控制、接纳控制和网络管理等。

博弈论是处理对抗性情况的有效方法。在安全设置、建模和攻防方面，这是一种流行的方法，例如网络安全、对抗干扰器的电子战、研究了国防EP行动成本等。

混合策略博弈论决策可以看作是有偏差的掷骰子：传统博弈中，决策者选择单一的最优行动，而在对抗性博弈中，决策者基于概率选择一个半随机行动，该概率是效用的函数。这种随机性使得对手更难预料行动。

要将博弈论融入电子战决策者，必须解决两个重要的挑战：(1)对敌方目标的理解(2)成本估计和比较。

在对抗性环境中，该方法依赖于对对手效用的估计。零和博弈假设每个参与者的损失和收益完全由其他参与者的损失或收益平衡。零和博弈可以用线性规划来求解。等价于电子战通常假设友军输了就是对手赢，但这不完全符合实际。

算法博弈论研究博弈论的计算方面，专注于寻找减少计算复杂性的解决方案。博弈论可以构造近似解或特定问题的解。

6.3 人机界面(HMI)

HMI设计需要具有直观性、灵活性、可扩展性和高响应性。人机界面系统的主要目标应该是(1)改善操作性能，(2)提高效率，(3)减轻任务规划者的任务量。应提供一套广泛、直观的显示和控制，以便操作员及时与电子战系统功能和数据交互。

通常，HMI将操作员操作转换为机器的命令操作，然后将机器的数据转换回人机操作员。在传统的HMI中，这些转换是静态的，不会根据操作员、机器或环境的状态而改变。

人机协作(HMT)弥补了这一差距：转换过程不再是静态的，可以使用人工智能和机器学习。HMT是人类操作员和机器之间的一种关系，它超越了人类操作或监督机器，操作员和机器是互补的团队成员。

人机交互的难点：

• 人体状态感知和评估；

• 人与机器之间的沟通和信息共享；

• 任务和认知建模：通过任务和功能分配建立工作量平衡；

• 人与机器：人与机器之间的适应性学习和扩展的相互训练；

• 数据融合和理解：整合人和机器数据，以生成共享的模型。

EBM系统部署每个节点的资源和动向。为了实现所有这些目标，EBM系统可以有多个应用HMT的HMI。

针对设计师、指挥官、任务规划者的HMI中各不相同。

系统设计人员可以提供：对任务类型、用户和平台的假设；决定系统的可控性和各项指标；ES的抽象特征构建；状态空间的缩减和优化指导；学习模型的类型；更改模型的形式；搜索启发式方法等。

挥官意图(CI)是整个电子战任务团队的一个重要概念，它描述了可接受的风险、可能的方法和成功条件等概念。

任务规划者和EWO必须能够指导和控制自动化，并理解所有反馈。

机器需要理解人类用户。使用偏好学习捕获用户的偏好。偏好学习方法可以学习效用函数，或者学习偏好关系。

6.4 结论

电子战规划系统必须在电子战计划的所有阶段为人工计划人员提供支持。

规划者必须处理行动和信息的不确定性，管理时间和资源限制。启发式学习和元学习有助于改进搜索过程。博弈论方法有助于团队合作管理和竞争对手。