基于智能优化算法解决多个干扰激励源的合成干扰波形优化问题,仿真目标为多参数的波形优化干扰。
代码如下:
SA_GA_PSO.m
clear;clc;%清除缓存
close all;
%%GA部分
NP=100; %种群规模
Dim=5; %维度
max_gen=800; %最大迭代次数
pop_max=2*pi; %位置边界
pop_min=0;
CR=0.6; %交叉概率 CorssRate
MR=0.05; %变异概率 MutationRate
fun_num=11; %测试函数中目标函数索引
%% 初始化种群
for i=1:NP
pops(i,:)=(pop_max-pop_min).*rand(1,Dim)+pop_min; %初始化种群
Obj_fun(i,:)=fun(pops(i,:),fun_num); %计算对应的目标函数值
end
Fitness=calculateFitness(Obj_fun); %计算适应性
[min_Obj_fun,index]=min(Obj_fun); %最小目标函数值及其索引
best_pop=pops(index,:); %最佳位置
%% 更新阶段
for gen=1:max_gen
%依据个体的适应性来更新选择概率
Prob=Fitness/sum(Fitness);
P=cumsum(Prob); %P是累加概率
%选择
for i=1:NP
r=rand; % 轮盘赌选择
j=find(r<=P,1,'first');
pops(i,:)=pops(j,:);
end
%交叉
for i=1:2:(NP-1)
r=rand;
if r<CR
point=ceil(rand*Dim);%取出一个维度
temp=pops(i,:); %个体i与个体i+1的几个(point到Dim)维度位置的交换
pops(i,point:Dim)=pops(i+1,point:Dim);
pops(i+1,point:Dim)=temp(1,point:Dim);
end
end
%变异
for i=1:NP
if(rand<MR)
muPoint=ceil(rand*(Dim));
pops(i,muPoint)= rand*(pop_max-pop_min)+ pop_min;
end
%计算更新后的个体的目标函数值
Obj_fun(i,:)=fun(pops(i,:),fun_num);
end
%更新适应性
Fitness=calculateFitness(Obj_fun);
%完成一代的更新
for i=1:NP
if Obj_fun(i)<min_Obj_fun
best_pop=pops(i,:);
min_Obj_fun=Obj_fun(i);
end
end
%记录
%pops
record(gen,:)=[gen,min_Obj_fun];
%disp(['Generation ' num2str(gen) ' Min Obj_fun= ' num2str(min_Obj_fun)]);
end
best_pop
min_Obj_fun
figure(1)
plot(record(:,1),record(:,2));
xlabel('迭代次数');
ylabel('效益函数值');
title('遗传算法收敛图');
%%画波形
t1 = 0:0.001:1;
f1 = [1 2 3 4 5];
ft = zeros(1,1001);
for j =1:length(best_pop)
ft= ft+cos(2*pi*f1(j)*t1+best_pop(j));
end
figure(2)
plot(t1,ft,"b")
hold on
%%SA部分
T=10000; %初始化温度值
T_min=1e-18; %设置温度下界
alpha=0.98; %温度的下降率
k=100; %迭代次数(解空间的大小)
Dim=5;
fun_num=11;
times=0;
x=getx; %随机得到初始解
while(T>T_min)
times=times+1;
for j=1:k
y=fun(x,fun_num);
x_new=getx;
y_new=fun(x_new,fun_num);%得到新解并求新的收益
delta=y_new-y;
if (delta<0)
x=x_new;%+(2*rand-1);
y_record(times)=y_new;
else
p=getp(delta,T);
if(p>rand)
x=x_new;%以概率p接受新解作为当前最优解
y_record(times)=y_new;
else
y_record(times)=y;
end
end
end
T=T*alpha;
end
disp('最优解为:')
disp(x)
y
times
%xx=1:times;
figure(3)
plot(y_record);
axis([1 times 2 6]);
xlabel('迭代次数');
ylabel('效益函数值');
title('模拟退火算法收敛图');
%%画波形
t1 = 0:0.001:1;
f1 = [1 2 3 4 5];
ft = zeros(1,1001);
for j =1:length(x)
ft= ft+cos(2*pi*f1(j)*t1+x(j));
end
figure(2)
plot(t1,ft,"g--");
hold on
%%PSO部分
Dim = 5; %维度
index=11; %测试函数索引
c1 = 1.4;
c2 = 1.4;
maxgen = 100; %进化次数
sizepop = 100; %种群规模
Vmax = 1;
Vmin = -1;
popmax = 5;
popmin = -5;
w=0.8;
record=zeros(1,maxgen);
%% 产生初始粒子和速度
for i = 1:sizepop
% 随机产生一个种群
pop(i,:) = (popmax-popmin)*rand(1,Dim)+popmin; %初始种群
V(i,:) = (Vmax-Vmin)*rand(1,Dim)+Vmin; %初始化速度
% 计算适应度
fitness(i) = fun(pop(i,:),index); %计算适应度
end
%% 个体极值和群体极值
[bestfitness bestindex] = min(fitness); %bestindex:全局最优粒子索引
gbest = pop(bestindex,:); %全局最佳位置
pbest = pop; %个体最佳
fitnesspbest = fitness; %个体最佳适应度值
fitnessgbest = bestfitness; %全局最佳适应度值
%% 迭代寻优
for i = 1:maxgen %代数更迭
for j = 1:sizepop %遍历个体
% 速度更新
V(j,:) = w*V(j,:) + c1*rand*(pbest(j,:) - pop(j,:)) + c2*rand*(gbest - pop(j,:));
%速度边界处理
V(j,find(V(j,:)>Vmax)) = Vmax;
V(j,find(V(j,:)<Vmin)) = Vmin;
% 种群更新
pop(j,:) = pop(j,:) + V(j,:);
%位置边界处理
pop(j,find(pop(j,:)>popmax)) = popmax;
pop(j,find(pop(j,:)<popmin)) = popmin;
% 适应度值更新
fitness(j) = fun(pop(j,:),index);
end
for j = 1:sizepop
% 个体最优更新
if fitness(j) < fitnesspbest(j)
pbest(j,:) = pop(j,:);
fitnesspbest(j) = fitness(j);
end
% 群体最优更新
if fitness(j) < fitnessgbest
gbest = pop(j,:);
fitnessgbest = fitness(j);
end
end
record(1,i)=fitnessgbest;
%fprintf('%d %f\n',i,fitnessgbest); %输出结果
% 收敛动图绘制存储
% plot(pop(:,1),pop(:,2),'*b')
% axis([popmin popmax popmin popmax])
% pause(0.1)
% x1=xlabel('x1');
% x2=ylabel('x2');
% title(['进化次数=' num2str(i)]);
% drawnow;
% frame = getframe(1);
% im = frame2im(frame);
% [A,map] = rgb2ind(im,256);
% if i == 1
% imwrite(A,map,'E:\测试图\标准PSO.gif','gif','LoopCount',Inf,'DelayTime',0.1);
% else
% imwrite(A,map,'E:\测试图\标准PSO.gif','gif','WriteMode','append','DelayTime',0.1);
% end
end
gbest
fitnessgbest
%% 适应度值变化绘图
figure(4)
plot(record);
xlabel('迭代次数');
ylabel('效益函数值');
title('模拟退火算法收敛图');
%%画波形
t1 = 0:0.001:1;
f1 = [1 2 3 4 5];
ft = zeros(1,1001);
for j =1:length(gbest)
ft= ft+cos(2*pi*f1(j)*t1+gbest(j));
end
figure(2)
plot(t1,ft,"r-.")
hold onfun.m
function y=fun(x,index)
% x代表参数,index代表测试的函数的选择
% 该测试函数为通用测试函数,可以移植
% 目录
% 函数名 位置 最优值
% 1.Sphere 0 0
% 2.Camel 多个
% 3.Rosenbrock
switch index
case 1 %Sphere函数
y=sum(x.^2);
case 2 %Camel函数,Dim只能取2
if length(x)>2
error('x的维度超出了2');
end
xx=x(1);yy=x(2);y=(4-2.1*xx^2+xx^4/3)*xx^2+xx*yy+(-4+4*yy^2)*yy^2;
case 3 %Rosenbrock函数
y=0;
for i=2:length(x)
y=y+100*(x(i)-x(i-1)^2)^2+(x(i-1)-1)^2;
end
case 4 %Ackley函数
a = 20; b = 0.2; c = 2*pi;
s1 = 0; s2 = 0;
for i=1:length(x)
s1 = s1+x(i)^2;
s2 = s2+cos(c*x(i));
end
y = -a*exp(-b*sqrt(1/length(x)*s1))-exp(1/length(x)*s2)+a+exp(1);
case 5 %Rastrigin函数
s = 0;
for j = 1:length(x)
s = s+(x(j)^2-10*cos(2*pi*x(j)));
end
y = 10*length(x)+s;
case 6 %Griewank函数
fr = 4000;
s = 0;
p = 1;
for j = 1:length(x); s = s+x(j)^2; end
for j = 1:length(x); p = p*cos(x(j)/sqrt(j)); end
y = s/fr-p+1;
case 7 %Shubert函数
s1 = 0;
s2 = 0;
for i = 1:5
s1 = s1+i*cos((i+1)*x(1)+i);
s2 = s2+i*cos((i+1)*x(2)+i);
end
y = s1*s2;
case 8 %beale函数
y = (1.5-x(1)*(1-x(2)))^2+(2.25-x(1)*(1-x(2)^2))^2+(2.625-x(1)*(1-x(2)^3))^2;
case 9 %Schwefel函数
s = sum(-x.*sin(sqrt(abs(x))));
y = 418.9829*length(x)+s;
case 10 %Schaffer函数
temp=x(1)^2+x(2)^2;
y=0.5-(sin(sqrt(temp))^2-0.5)/(1+0.001*temp)^2;
case 11 %干扰适应度函数
t = 0:0.001:1;
f = [1 2 3 4 5];
radar=zeros(1,1001);
for i = 1:length(x)
radar = radar+cos(2*pi*f(i)*t+x(i));
end
radar_abs = abs(radar);
y = max(radar_abs);
otherwise
disp('no such function, please choose another');
endgetx.m
function x=getx
Dim=5;
for i = 1:Dim
x(i)=2*pi*rand;
end
endgetp.m
function p=getp(c,t)
p=exp(-c/t);
endcalculateFitness.m
function Fitness=calculateFitness(fObjV)
ind=find(fObjV>=0); %如果目标函数值不为负
Fitness(ind)=1./(fObjV(ind)+1);
ind=find(fObjV<0); %如果目标函数值为负
Fitness(ind)=1+abs(fObjV(ind));仿真结果
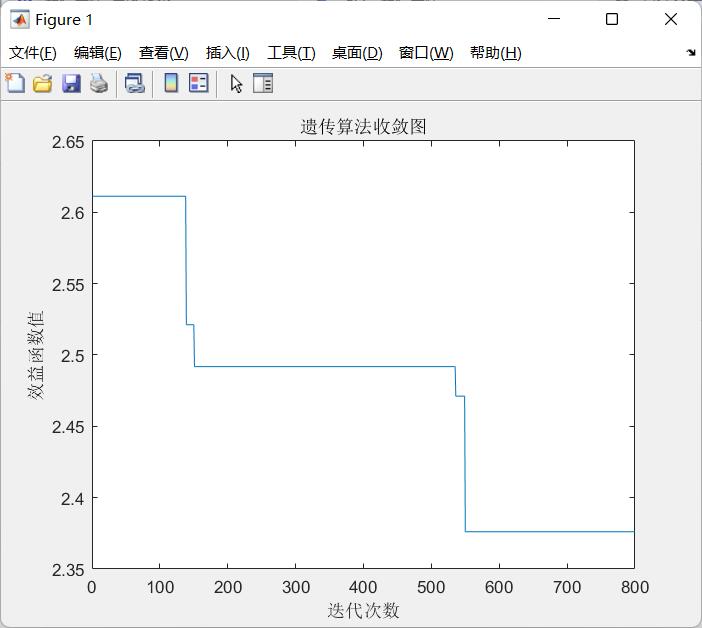
GA算法收敛图
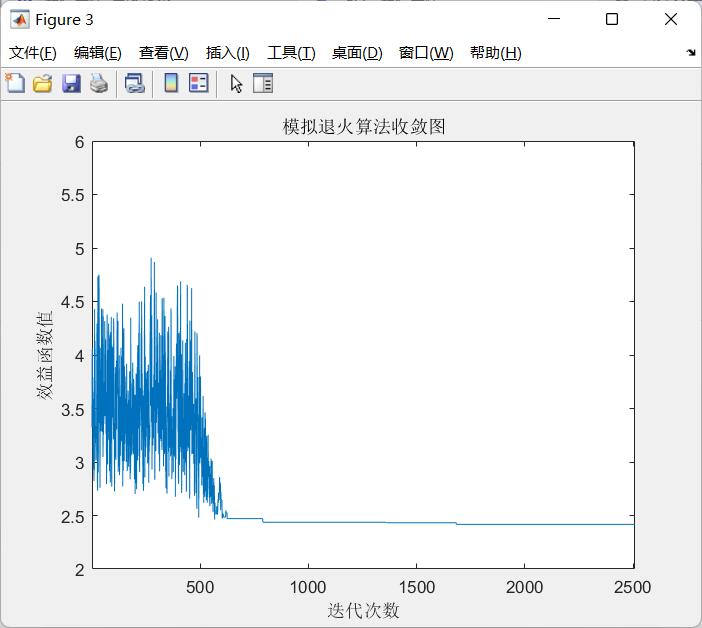
SA算法收敛图
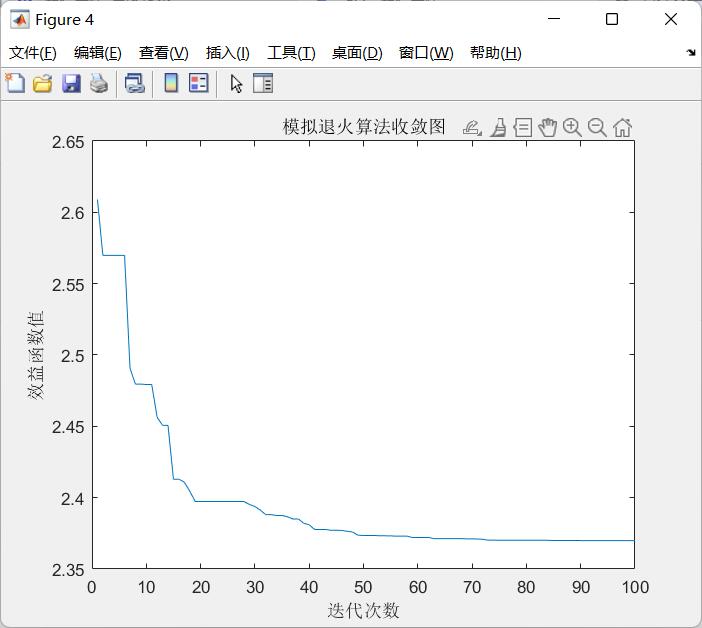
粒子群优化算法收敛图(图中文字有误)
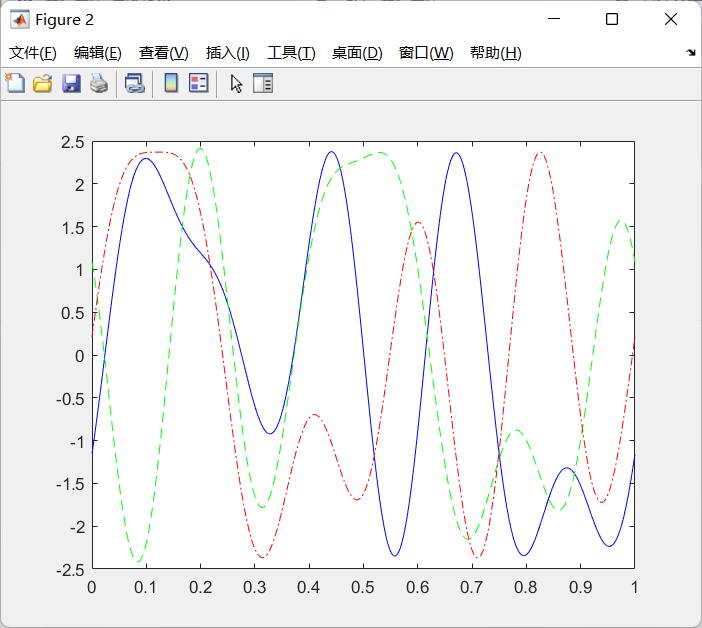
三种波形合成图
结果分析
用matlab对《认知电子战原理与技术》4.3.3节“自适应的干扰波形优化”进行了仿真,基本完成了复现。主要包括GA遗传算法、SA模拟退火算法、PSO粒子群优化算法三种,采用功率利用率作为适应度函数。得到的最佳相位分别为[3.5881 2.8670 2.9428 4.3782 0.7402]、[ 3.0420 4.6321 6.2296 3.6424 2.3906]、[0.6512 -0.7903 3.6211 0.0018 1.6819],函数收敛值分别为2.4630、 2.4012、2.3829。合成波形中,蓝线、绿线、红线分别代表GA,SA,PSO算法的波形。
可以看出遗传算法的迭代次数最短,但收敛值也最大,模拟退火算法和粒子群优化算法收敛需要的次数更高,但可以一定程度上找到全局最优解。
hh
huawei 2025-03-24